|
Snail Trail Reflection
The snail trail was a GeoGebra lab that used reflection and points to reflect the movement of each point. Each point move in sync with the other. I noticed that all points moved together as a reflection over three line of reflectional symmetry that I set down before the final piece. These lines are the lines that each point reflects around. |
|
Tessellations
Draft 1 of tessellation. Finale tessellation tile.
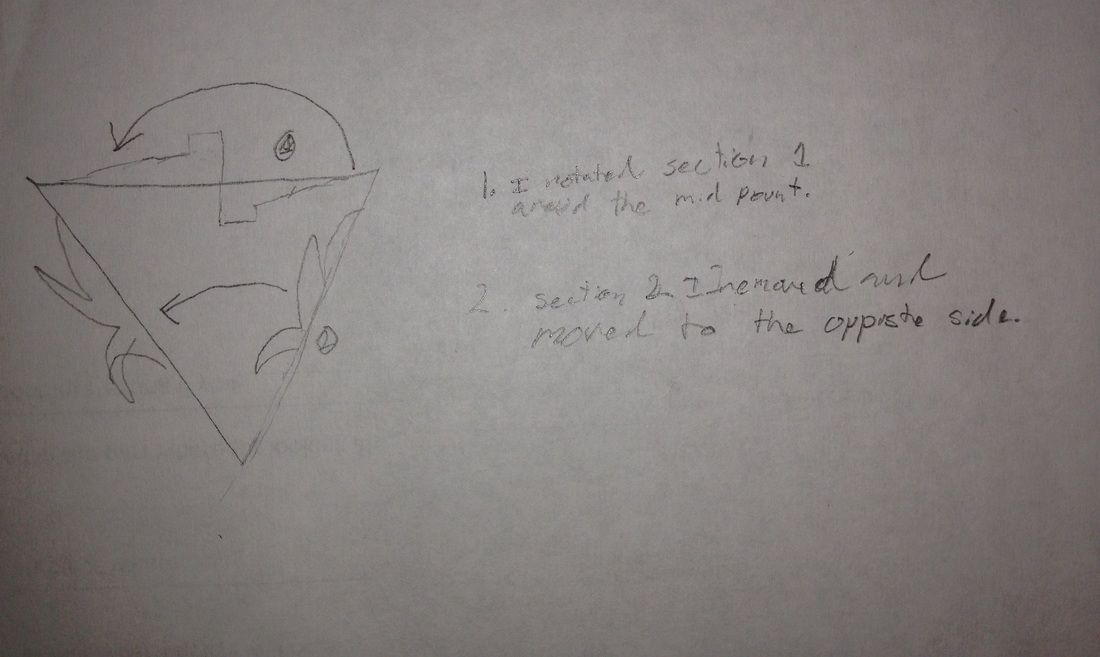
My Theme: My Them for the tessellation project is no really a theme but more of two colors alternating in the form of a random shape formed from a equilateral triangle. I didn't really have a idea for a theme and the creativity wasn't flowing so I just used the shape and worked with it.
The creation; With my tessellation I started with the basic equilateral triangle and expanded extrapolated the finale shape. How I reached the finale form was by first cutting out the part that looks kinda like Sidney opera House and adding it to the side directly below it. I then cut out the part that looks like a boot on the side that had not been cut into yet and rotated the boot counterclockwise 180 degrees. This made look like it part of monument valley not a boot. This how I created the tessellation that I used for my tessellation project.
I see tessellations as more of an art form then a math form. Not much math goes into the creation of the tessellation. There is no equations or complicated math, mostly it basic logic and requires you to be able to form and create shapes in your head. I think this is mostly an art form because I don't think of math as pictures but as numbers and letters representing the value of objects.
Mc Escher saw tessellation as art and math together and was able to use this to create a art form that became famous.
Mc Escher saw tessellation as art and math together and was able to use this to create a art form that became famous.
The burning tent problem.
Unit 3
Q1: What content/skills have been most interesting to you?
The skills that I have most connected with this year in math have been surface area and how it relates to volume of different shapes. This unit has started me off on the path for basic engineering and design for many areas. For one anything that has surface area or requires a knowledge surface area.
Q2: How have you grown mathematically?
I have grown mathematically in many areas this year. For starters I have learned and studied how surface area and volume are related and how one changes the other. Other areas that I have grown in are systems of equations and how to correctly solve them for the answer.
The skills that I have most connected with this year in math have been surface area and how it relates to volume of different shapes. This unit has started me off on the path for basic engineering and design for many areas. For one anything that has surface area or requires a knowledge surface area.
Q2: How have you grown mathematically?
I have grown mathematically in many areas this year. For starters I have learned and studied how surface area and volume are related and how one changes the other. Other areas that I have grown in are systems of equations and how to correctly solve them for the answer.
The burning tent problem questions.
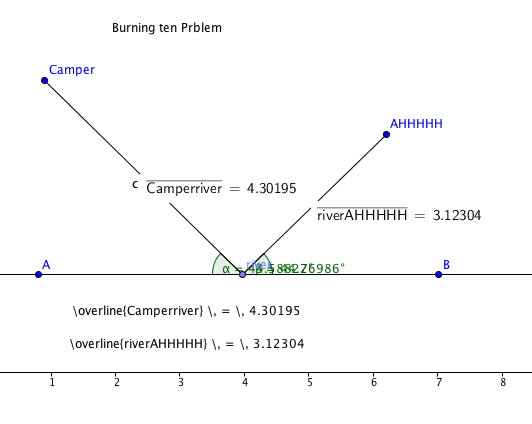
Q.Once you have the minimal path, what appears to be true about the incoming angel and the out going angel?
1.The angels become the same when the distances from the Camper to the Tent shortens the smallest possible distance.
Q.Why is the segment from Camper to tent the shortest path?
2.The reasons the distances is shorter is because the distance from the Camper to the river and the river to the tent is exempt from the distance traveled.
Q.Where should point river be located in the relation to the segment Camper to Tent and line AB so that the sum of the distances is minimized?
3.The river point should be located directly in the middle of point Camper and the Tent to make the distance as short as possible. For me the point was closer to the middle but lightly closer to the tent. The angels were both 44 degrees and were exactly the same.
Q.Once you have the minimal path, what appears to be true about the incoming angel and the out going angel?
1.The angels become the same when the distances from the Camper to the Tent shortens the smallest possible distance.
Q.Why is the segment from Camper to tent the shortest path?
2.The reasons the distances is shorter is because the distance from the Camper to the river and the river to the tent is exempt from the distance traveled.
Q.Where should point river be located in the relation to the segment Camper to Tent and line AB so that the sum of the distances is minimized?
3.The river point should be located directly in the middle of point Camper and the Tent to make the distance as short as possible. For me the point was closer to the middle but lightly closer to the tent. The angels were both 44 degrees and were exactly the same.
Problem of the week
Unit 2 Reflection: Shadows, Similarity and Right Triangle Trigonometry
Q1: What has been the work you are most proud of in this unit?
During my time studying I have not found a problem of the week that I like, or find interesting to me personally. I have found though, that each had a deeper meaning, more then just added work. Each Pow has been an assessment of my learning and how I face problems that I attempt to solve.
Q2: What skills are you developing in geometry/math?
In geometry I have been developing my skills in critical thinking and problem solving. After spending time in both algebra and geometry I have attempted to develop these skills. These skills are considers 21st century skills that are used in are life and are extremely useful.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you.
Trigonometry. Trig is the understanding of angle relationships and the ability to find angles and side length through the process of trigonometry. The uses of trig range from problem solving in simulation to hands on approach to larger problems using measurements taken for that situation.
Q1: What has been the work you are most proud of in this unit?
During my time studying I have not found a problem of the week that I like, or find interesting to me personally. I have found though, that each had a deeper meaning, more then just added work. Each Pow has been an assessment of my learning and how I face problems that I attempt to solve.
Q2: What skills are you developing in geometry/math?
In geometry I have been developing my skills in critical thinking and problem solving. After spending time in both algebra and geometry I have attempted to develop these skills. These skills are considers 21st century skills that are used in are life and are extremely useful.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you.
Trigonometry. Trig is the understanding of angle relationships and the ability to find angles and side length through the process of trigonometry. The uses of trig range from problem solving in simulation to hands on approach to larger problems using measurements taken for that situation.
Problem of The Week
Problem of the Week
Austin Munroe, Lauren Brown
1/15/15
Kneller
P.O.W #1
The problem, was to take a circular pie and cut through it, each line must be straight and start at one side of the pie and go completely through it. The line do not have to go through the center but must go through without stopping. The idea is to start with one line and build from that, growing from one to two and from two to three. As you cut each line you attempt to maximize the number of pieces from the cuts. The size of the pieces does not matter, the problem is to get as many pieces of the pie with a set number of cuts, in this case, one, two, three, four and five.
The thought process that we had while beginning this POW was to begin with a circle and cut lines through it and create as many pieces as we could, which we did. We started by drawing a complete pie circle and cutting the maximum number of pieces we could at random until a pattern was found. We found that beginning with the one cut and then crossing it with another was the best way to start. And then crossing these again in an area where it would intersect both lines created 3 extra pieces bring the total number of pieces to 7. Continuing the process of crossing the cuts made before eventually leads to the final solution for 5 cuts. We looked for a pattern in the table that we created with the data we found. The pattern we came up with was beginning with 1 cut creating 2 slices. The number of slices that were created was then added to the next number of cuts going up by one on the number line. This gave you the next maximum number of slices for the cuts that was just added to the earlier number of pieces.
The solution is simple and yet challenging. Each cut made in the pie must cross the cuts set down before it. Not only that, but it must cross every line to reach the maximum number cuts in a way to make as many spaces in the areas where the lines intersect. The pattern we came up with to find the largest number of pieces for a given number of cuts was that it grew by adding the most recent number of slices to the next amount of cuts. The formula that we came up with to find the largest number of slices for a number of cuts without having to find all the number of slices in between was .5x2 + .5x + 1. We tested this formula with our table and found that it was an accurate formula to find the largest number of sliced for a number of cuts.
Possible extensions for this problem would be to change how the cut can cross each other. For example on certain lines can be cross is different places, like in the middle of each cut. Another idea is make that you can only cut the line as a perpendicular bisector of the last line.
One of the first reactions I(Lauren) had while working on this problem was I thought that it would be really easy to just make as many straight lines through the pie to create different slices and pieces. It turns out that there were a lot of different ways to draw an additional line to the already existing lines that either created several new slices or just a few. I thought that this problem was educationally worthwhile because it taught me how to maximize numbers that are produced by single lines. I also learned about different equations that can be used for the same problem; and last I learned how to find simple patterns that continue through a table. I think that this POW could be changed for the better by being given a more clear and straightforward equation. I did enjoy working on this problem, I thought that it was very fun to learn how to maximize products. This problem of the week was not too easy or too hard, I thought that it was challenging but not too challenging. Out of a score of 25 pts. I would give myself and Austin a 22-25 because of the time and effort that we spent working hard on this POW.
Austin Munroe, Lauren Brown
1/15/15
Kneller
P.O.W #1
The problem, was to take a circular pie and cut through it, each line must be straight and start at one side of the pie and go completely through it. The line do not have to go through the center but must go through without stopping. The idea is to start with one line and build from that, growing from one to two and from two to three. As you cut each line you attempt to maximize the number of pieces from the cuts. The size of the pieces does not matter, the problem is to get as many pieces of the pie with a set number of cuts, in this case, one, two, three, four and five.
The thought process that we had while beginning this POW was to begin with a circle and cut lines through it and create as many pieces as we could, which we did. We started by drawing a complete pie circle and cutting the maximum number of pieces we could at random until a pattern was found. We found that beginning with the one cut and then crossing it with another was the best way to start. And then crossing these again in an area where it would intersect both lines created 3 extra pieces bring the total number of pieces to 7. Continuing the process of crossing the cuts made before eventually leads to the final solution for 5 cuts. We looked for a pattern in the table that we created with the data we found. The pattern we came up with was beginning with 1 cut creating 2 slices. The number of slices that were created was then added to the next number of cuts going up by one on the number line. This gave you the next maximum number of slices for the cuts that was just added to the earlier number of pieces.
The solution is simple and yet challenging. Each cut made in the pie must cross the cuts set down before it. Not only that, but it must cross every line to reach the maximum number cuts in a way to make as many spaces in the areas where the lines intersect. The pattern we came up with to find the largest number of pieces for a given number of cuts was that it grew by adding the most recent number of slices to the next amount of cuts. The formula that we came up with to find the largest number of slices for a number of cuts without having to find all the number of slices in between was .5x2 + .5x + 1. We tested this formula with our table and found that it was an accurate formula to find the largest number of sliced for a number of cuts.
Possible extensions for this problem would be to change how the cut can cross each other. For example on certain lines can be cross is different places, like in the middle of each cut. Another idea is make that you can only cut the line as a perpendicular bisector of the last line.
One of the first reactions I(Lauren) had while working on this problem was I thought that it would be really easy to just make as many straight lines through the pie to create different slices and pieces. It turns out that there were a lot of different ways to draw an additional line to the already existing lines that either created several new slices or just a few. I thought that this problem was educationally worthwhile because it taught me how to maximize numbers that are produced by single lines. I also learned about different equations that can be used for the same problem; and last I learned how to find simple patterns that continue through a table. I think that this POW could be changed for the better by being given a more clear and straightforward equation. I did enjoy working on this problem, I thought that it was very fun to learn how to maximize products. This problem of the week was not too easy or too hard, I thought that it was challenging but not too challenging. Out of a score of 25 pts. I would give myself and Austin a 22-25 because of the time and effort that we spent working hard on this POW.
Austin Munroe/Ben Glennjman
4/3/2015
Caitlyn keneller
6
POW #5
The problem given to us for this assignment, was to find the most cost effective size for a 12 ounce soda can. This problem is broken down into three steps. This first is the radius, the second is the height and the third is the surface area. Using the radius, height and surface area we can find the perfect size for a 12 ounce soda can that uses the least amount of material to provide the most cost effective product.
For finding the solution to this problem we started by selecting 7 different radius that Ben and I thought would be the closest to the ideal size. Then we took the equationh=355/(r2)which finds the height for a 12 ounce canister with that specific radius, we used this to find the corresponding height for each radius that we picked. By doing this we got the height for each radius and the next part of the process lined up. The next step requires the use of another equation to find the surface area using the radius and height. By taking the height and radius and plugging it into the equation SA=2r2+2rhGives us the surface area for that size container. Ben and I both did this for the radius of 3, 4, 5, 6, 7, 8, 9, and 10. Using the equations, we found that out of these, 4 had the smallest surface area out of the whole numbers we used. Going further we broke them down in between the numbers 3 and 4 to the tens place, 3.9, 3.8, 3.7, 3.6. We then ran the same process for these numbers and found that a radius of 3.8 was the lowest surface area for a 12 ounce soda can. This gave us the most cost effective can with the lowest surface area down the the tens place.
The solution we found for this problem was a radius of 3.8cm and a height of 7.825485429cm got us the a low surface area of 277.5713011cm. This was the lowest that we got and in my opinion is the most reasonable answer for the problem. We found the lowest possible answer down to the tens place which in my mind is as reasonable as anyone would go to save money on soda can production.
The results that we got from the equations we used seam to the height and radius of the current soda can used today. As the radius became larger the height shortened and vis versa, when the height got larger the radius. The proportions of our changing soda can seamed to be similar to that of a standard soda can. I think the reason for this is because the standard soda can which has a radius of 2.75cm and a height of 12.5cm is very close to what our improved version of 3.8cm radius and 7.8cm tall. It is our belief that our results are very close to the best and that compared to a normal soda can are very close in proportion.
During the duration of this project we became more involved with solving equations and plugging in real numbers into equations to get results. In our opinion we already had experience with these types of equations and were able to finish this problem with more ease than other, this being said we both feel that our knowledge we had before has been increased and solidified into our mathematical processing abilities that we already possessed. All and all this assignment helped us increase our skills with equations and how to transcribe the data we gathered into a usable form that could be applied to a variety of situations both in secondary learning and employment after are school.
4/3/2015
Caitlyn keneller
6
POW #5
The problem given to us for this assignment, was to find the most cost effective size for a 12 ounce soda can. This problem is broken down into three steps. This first is the radius, the second is the height and the third is the surface area. Using the radius, height and surface area we can find the perfect size for a 12 ounce soda can that uses the least amount of material to provide the most cost effective product.
For finding the solution to this problem we started by selecting 7 different radius that Ben and I thought would be the closest to the ideal size. Then we took the equationh=355/(r2)which finds the height for a 12 ounce canister with that specific radius, we used this to find the corresponding height for each radius that we picked. By doing this we got the height for each radius and the next part of the process lined up. The next step requires the use of another equation to find the surface area using the radius and height. By taking the height and radius and plugging it into the equation SA=2r2+2rhGives us the surface area for that size container. Ben and I both did this for the radius of 3, 4, 5, 6, 7, 8, 9, and 10. Using the equations, we found that out of these, 4 had the smallest surface area out of the whole numbers we used. Going further we broke them down in between the numbers 3 and 4 to the tens place, 3.9, 3.8, 3.7, 3.6. We then ran the same process for these numbers and found that a radius of 3.8 was the lowest surface area for a 12 ounce soda can. This gave us the most cost effective can with the lowest surface area down the the tens place.
The solution we found for this problem was a radius of 3.8cm and a height of 7.825485429cm got us the a low surface area of 277.5713011cm. This was the lowest that we got and in my opinion is the most reasonable answer for the problem. We found the lowest possible answer down to the tens place which in my mind is as reasonable as anyone would go to save money on soda can production.
The results that we got from the equations we used seam to the height and radius of the current soda can used today. As the radius became larger the height shortened and vis versa, when the height got larger the radius. The proportions of our changing soda can seamed to be similar to that of a standard soda can. I think the reason for this is because the standard soda can which has a radius of 2.75cm and a height of 12.5cm is very close to what our improved version of 3.8cm radius and 7.8cm tall. It is our belief that our results are very close to the best and that compared to a normal soda can are very close in proportion.
During the duration of this project we became more involved with solving equations and plugging in real numbers into equations to get results. In our opinion we already had experience with these types of equations and were able to finish this problem with more ease than other, this being said we both feel that our knowledge we had before has been increased and solidified into our mathematical processing abilities that we already possessed. All and all this assignment helped us increase our skills with equations and how to transcribe the data we gathered into a usable form that could be applied to a variety of situations both in secondary learning and employment after are school.
POW reflections
Problems of the week have helped me to grow in many ways over the course of this year. POWS offer an in depth explanation to the field that they cover. Each POW gave me the understanding to learn and grow in each area that we were studying. Because of POWs I know that I have have the skills and knowge to succeed in each topic.
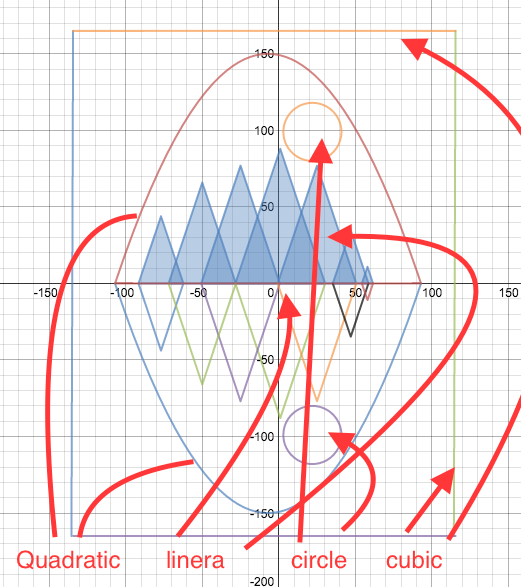
Desmos Drawing and Function Families
|
|